Why Math?

No, not why does math exist. That question is actually relatively easy to deal with.

Once upon a time I did a major in the subject. Later I spent nearly two decades teaching math to middle and high school students. Or trying to. Which means I have a pretty good idea of how mathematics developed over the centuries and how it’s used in the real world.

My question is why do we teach math as an independent subject in school? Why is the math curriculum used in most schools structured in the way that it is?

And why do we consider math so damn important that every kid needs to spend a large chunk of their academic time on the subject?

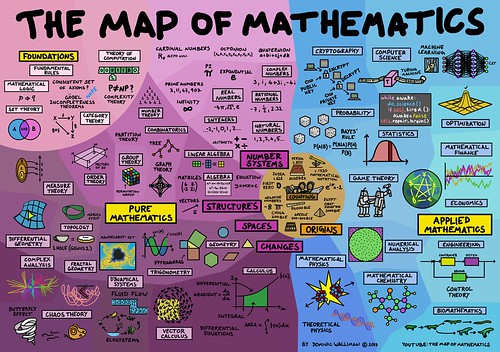
Let’s start with the curriculum. Take a look at that chart at the top.

Students in most American schools spend almost their entire time in K12 math swimming around in that purple area in the left two-thirds of the page. Most often working through assignments that place a heavy emphasis on arithmetical operations and computation, employing a very mechanical approach to the subject.

When you took Algebra 1, and I’m pretty sure you did since almost no one graduates from high school without it, do you remember deriving the quadratic formula? Or performing a two-column proof in Geometry class? Or dividing two fractions somewhere in elementary school?

I’m willing to bet you don’t. At least not the specifics, despite spending many long hours of school math practicing the algorithms provided the text book. I hope you at least remember the sympathetic teacher with the weird sense of humor who was constantly trying to find new ways to make the subject more interesting. :-)

However, almost all students would be far better prepared for college (or whatever else might have come after graduation), if they spent less time cranking through the mechanics of math and more time on the stuff in the blue space.

Playing with more realistic problems and learning how math is applied and actually used in the real world. Not doing math in a “math class” and instead using it as a tool to solve problems in science, engineering, and social studies. Maybe even music.¹

When it comes to learning mathematics, every educated person needs a solid foundation in numeracy, which the dictionary defines as “ability to understand and work with numbers”. Those concepts and processes involved with probability, statistics, economics, and the other math-related stuff that confront all of us every day.

Instead, with very few exceptions, the K12 math curriculum from about the third grade on is focused entirely on getting kids into and through Calculus. A branch of mathematics buried deep in the purple space that very few people in the world actually need or use.

Even for people who go on to work in science and engineering fields, the Calculus and other mathematics is done by a computer. Their job doesn’t involve cranking through the algorithms by hand. They determine the correct input based on the problem parameters and then figure out how to apply the output correctly to solve that problem. Which far too often has more than one possible solution.

Then there’s another part of the original question: why does math occupy such a central place in K12 education? A writer for the UK-based news site The Guardian offers one explanation.

The cult of maths² knows no bounds. It rules global education like no other subject, its status akin to medieval Latin. The reason is that it is so easily measurable. Maths is right or wrong. Its targets are international, its results classifiable, its league tables definitive for any government. Immune to leftwing bias and rightwing ideology, maths can run like a ramrod through every school worldwide, a statistician’s dream.

Before the middle of the 20th century, Latin and math were subjects considered core for any student receiving a “classical” education. After World War II, Latin faded quickly from the curriculum while math’s position solidified and grew. However, the way math was taught changed very little over time.

The Guardian writer hits on one major reason for that calcification: school math is easy to test and thus to quantify the scores, as well as comparing students, states, and countries. The math actually used in the real world to solve problems (that stuff in the blue) is far less exact.

As is the answer to question “why math” that started all this rant.

Somewhere in the evolution of the K12 math curriculum, it was decided that this approach was best for students. That it would produce the mathematical knowledge students needed for college and/or “real world” jobs. And that studying math will help kids become logical thinkers. Which is an even more farcical justification, requiring far more time, space, and snark to discuss.

Anyway, this is a topic I’ve had swimming around in my head for a long, long time. Some version of this post has been sitting in my edit box for nearly four years and, at times, it was much longer, not to mention far more disjointed and unreadable than this first pass.

Feel free to let me know just how wrong I am.

The Map of Mathematics poster was created by Dominic Walliman and posted to his Flickr page. Dominic has a large collection of similar works dealing with various scientific subjects. He also sells wall posters of each and I wish I could have stuck one of these up in my classroom.

1. How about if we remove math from STEM, weave that subject into the S, T, and E, and make the M be music instead?

2. People in the UK rightly refer to “maths”, the plural, because there are multiple branches of mathematics.