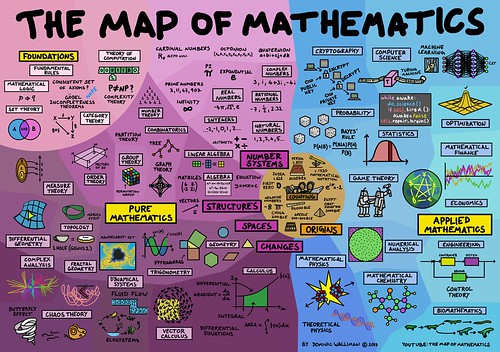
That’s not just an intriguing question, it’s also the title of a very interesting book. I highly recommend it for anyone with an interest in math.
But I also think it would be good for those of you who say you are not a “math person”. Offering a little insight into why school soured you on the subject.